作成日 2007/7/13
最終更新日 2009/11/15
関連
クラス間の関係には、依存、関連、集約、コンポジション、汎化、実現（他にあるかなぁ。）があります。
（クラス図（※１）においてクラスとクラスを結んでいる線だと思ってください。）
ここではクラス間の関係のうちのひとつである、関連（association）について説明します。
「
クラス図とER図とクラスの抽出
3.クラス図とER図の関係
」(クリックすると別ウィンドウで表示します)に関連とはER図におけるリレーションシップと同じようなものと書きました。意味的にはこれは間違いではありませんが、これだけですと（多分）クラス図を元にプログラミングすることが出来ないと思います。
このページでは関連と属性の関係について説明し、さらに、より関連についての理解を深めてもらうために（※２）、関連について初心者がつまづくと思われる1つのクラスへ関連の線が2本ある場合や自分自身に関連の線が引いてある（自己再帰関連）場合について説明します。
※１：UMLのバージョンは2.0とします。
※２：「より関連について理解を深めてもらうために」と書いたが、混乱するだけという可能性もある。そのときは、ごめん…。
実は、関連端（association
end）と属性（attribute）を総称してプロパティ（property）と呼びます。
まったく意味を変えずに、属性を関連・関連端に変換することが可能です。
意味を多少削れば、関連・関連端から属性に変換することも可能です（※１）。
結局、関連とは属性のようなもの(まったく同じではない)だと考えてOKです。
実際に、クラス図を元にJavaやC++、エクセルVBAでプログラミングするときは、関連端はクラスの属性としてプログラミングします。
例えば、図１のクラス図と、図２のクラス図は同じ意味です。
図１ 電話帳のサンプルのクラス図
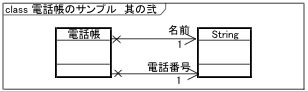図２ 電話帳のサンプルのクラス図（図１の属性を関連・関連端に直した。）
図３のクラス図と、図４のクラス図はだいたい同じ意味です（まったく同じ意味ではありません）。
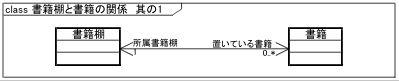図３ 書籍棚と書籍の関係を表したクラス図（双方向関連を使用して表記）
図４ 書籍棚と書籍の関係を表したクラス図（属性を使用して表記）
※１：「まったく意味を変えずに、属性を関連・関連端に変換すること」は、恐らく間違いではないのですが、
その逆である、「まったく意味を変えずに、関連・関連端から属性に変換すること」は必ずしも可能とは限りません。
属性よりも、関連・関連端のほうが表現能力があるため、多少（？）、表現内容を削らないと変換できない場合があります。
関連・関連端で表現が可能で、属性に表現ができないものとして、限定子、双方向関連(※２)、関連クラスなどがあります。
※２：双方向関連を属性に変換すると、一見可能なように見えるのですが、対応関係が分からなくなるということが起こります。
一般的なUMLの書籍を見ても、2つのクラスが2つの関連の線で結ばれているという例は多くはないようです（※１）。
UML
2.0の仕様書を見ると、2つのクラスが2つの関連の線で結ばれているという例は少なくないです（例えば p28 Figure
7.11）。
意味が良く分からなければ、関連・関連端を属性に直して考えてみると良いです。
次の2つのクラス図は同じ意味です。
図５ 電話帳のサンプルのクラス図
図６ 電話帳のサンプルのクラス図（属性を関連・関連端に直した。）
-----
※１：いや、実は、いろんなところにあるのですが、気がつかない。
UML
2.0の仕様書を見ると、自己再帰関連はいたるところにあります（例えば p23 Figure 7.3）。
自己再帰関連があるとは同じクラスの別のオブジェクト（自分自身の場合もある）への参照を持っていることを表します。
自己再帰関連の意味が良く分からなければ、関連・関連端を属性に直して考えてみると良いです。
例を挙げます。
例：単方向リスト（※１）
単方向リストとは、早い話、可変長の配列です。
C言語でプログラミングをするときは、使うこともあるかもしれません。
エクセルVBAではCollectionクラスという便利なクラスがあるので、単方向リストを聞いたことが無い人が多いと思いますので、簡単に説明します（※２）。
繰り返しになりますが、単方向リストは、早い話、可変長の配列です。また、データ追加や削除が簡単に行えます。データの追加や削除は一番最後のデータのみしか出来ないなんてことはありません。
イメージとしては次のようになります。
図７ 単方向リストのイメージ図（※UMLの図ではありません。）
途中にデータを追加する場合は、次のようになります。
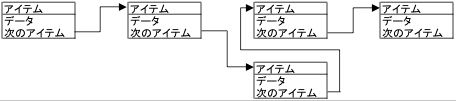図８ 単方向リストの途中にデータを追加する場合のイメージ図（※UMLの図ではありません。）
途中のデータを削除する場合は、次のようになります。
図９ 単方向リストの途中のデータを削除する場合のイメージ図（※UMLの図ではありません。）
で、この単方向リストについてクラス図を書くと、次の２つのどちらか（どちらでも良いですが、普通は右側の図）となります。
 |
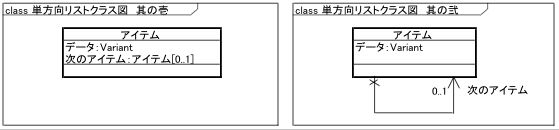図１０ 単方向リストのクラス図
左の図の次のアイテム属性（右の図では次のアイテム関連端）の多重度が
1ではなく0..1（0から1）となっているのは最後のデータは次のデータへの参照を持たないためです。
（C言語ならNULL、エクセルVBAならNothingとなります。） |
※１：単方向リストの勉強は基本情報技術者試験の午後試験対策になりますので、取得を考えている人は勉強しておいた方がよいです。
でも、だるまは基本情報技術者を受験したときは単方向リストを知りませんでした。知っていないと合格できないということはありません。
※２：そういう、だるまも、ごく最近まで「単方向リスト」を知りませんでした…。
このページを作成するのに参考にしたページです。
ただし、だるまは、このページを作成するにあたり、これらのページを100%理解してから作成したわけではない（おいおい。）です。
間違い（リンク先のページではなく、このページに）があったら、ごめんなさい。
このページの利用によって発生した、いかなる損害について、このホームページの作成者は責任を負いません。
このページの間違いや嘘を見つけた方、このページに書いて欲しい情報がある方は
メールをお願いします。
Microsoft 、Windows 、Visual Basic および Excel は米国Microsoft
Corporationの米国およびその他の国における登録商標または商標です。
ここではExcel® をエクセル、Visual Basic® for Applications をVBAと表記する場合があります。
Mac 、Mac OS 、Mac OS X は米国Apple
Computer,Inc.の登録商標または商標です。
OMG、UML、Unified Modeling
Languageは、Object Management Groupの商標または登録商標です。
JavaおよびJavaに関する商標は、米国およびその他の国における米国Sun Microsystems, Inc.の商標または登録商標です。
その他、社名および商品名、システム名称などは、一般に各社の商標または登録商標です。
このホームページの作成者はこれらの会社とはいっさい関係がありません。
