効率の悪い方法でも良い

作成日　2013/10/5
最終更新日　2013/10/9

　このページでは情報処理技術者試験対策の計算問題の対策です。このページでは効率が悪い方法で解いても良いということを説明します。

1.はじめに
2.余事象を使わない
3.実際に数値を入れて確認する
4.2進数の計算をそのまま行わない

1.はじめに

　まず、「効率の悪い方法で良い」を説明する理由が、分からないだろうと思う。なので、これについて説明します。

　これを読んでいる人は、試験時間は限られているから、「効率の良い方法で解くのが良い」と思っているでしょう。

　まあ、気持ちは分かります。しかし、だるまはこれに対してNOを突きつけます。

　理由を説明します。

だるまは数学が得意です。実用数学技能検定1級を持っています。しかし、効率の良さにこだわるということはしていませんでした。というか、だるまは、あまりにも暗記がダメ過ぎて、数学の公式をなかなか覚えられませんでした。なので、試験中に数学の公式を自分で導き出す始末です（※簡単なものに限る）。これのどこが、「効率が良い」のだろうか？です。
それと、多少効率は悪くても、汎用的に使える方法を覚えるようにしていました。この方が暗記しなければならない量が減るためです。
上記のことから考えると、「効率の良い方法」は「暗記を必要とする」ことが多いです。多少、効率が落ちても良いので、暗記は減らした方が良いでしょう。というのも、情報処理技術者試験は暗記しないといけないことはたくさんある（ネットワークやセキュリティ、法律等）ためです。そういう、勉強時間まで考えた効率の良さを考えると、問題を解くのに必要な時間が増えてしまっても、良いという答えになります。
自分が納得いく方法で解くのが良いです（※出来れば、論理的に正しいやり方が良い）。
「2.余事象を使わない」はこれの代表格です。高校数学で余事象を習うと、それ以降、問題に対する解説は、余事象で解けるものは全て余事象で解くようになり、余事象を使わない方法で解くやり方では一切解かなくなります。しかし、もし、余事象を使うということが分からなかったら、あるいは、納得いかなかったらどうするのか？１つの解法しか示さないというのはそれに、答えていないです。
ということで、例としてあげてます。
自分が納得いく（理解できる）やり方は、人それぞれです。人に、「効率が悪い」と言われても良いでしょう。
いやいや、と言う方がいると思うので、多くの人（というか、情報処理試験の解説サイト）が、効率の悪い方法を採用している例として「3.実際に数値を入れて確認する」をあげました。

このページのトップへ

　余事象というのは、確率の計算をするときの考え方の1つです。
　例えば、ある確率を求めたら、それが起こらない確率は、1からその確率を引けば良いことになります。
　え？だから何なのか？って。
　余事象を使わないで計算することは、かなり大変ですが不可能ではないです。やってみましょう。　まずは、例を示します。

■問題：表と裏の区別が付くコインが2枚ある。2枚とも投げて、最低でも片方のコインが裏である無い確率はいくらか？なお、コインを投げて、表、裏となる確率は共に1/2であるとする。

■正答：3/4
■解説：
◆まず、余事象を使った方法で答えを出してみます。
　「最低でも片方のコインが裏である無い確率」ということは
　　1 - 両方のコインが表になる確率
　なので、1 - 1/4となり、結果、3/4となります。

◆次に、余事象を使わない方法で出してみます。
　「最低でも片方のコインが裏である無い確率」ということは、以下の2通りが考えられます。
　　　(1)両方とも裏
　　　(2)片方が裏で、もう片方が表
　上記2つの確率をそれぞれ、求め、合計すれば、求めたい確率が計算できます。
　(1)の確率は1/4となります（計算式は1/2 * 1/2です）。　(2)の確率を間違える人が多いのですが、1/2になります。なぜか、ですが、これはコインに名前をつけると分かります。コインAとコインBとします。すると、「片方が裏で、もう片方が表」というのは、
　　　コインAが裏でコインBが表。
　　　コインAが表でコインBが裏。
　の2通りがあることが分かります。共に確率は1/4（計算式は1/2 * 1/2です）ですから、1/4 + 1/4で1/2となります。
　そうしたら、(1)の確率と(2)の確率を合計して、
　　1/4 + 1/2 = 3/4
　が得られます。

◆もうひとつ、表を使った解き方も説明しておきます（このサイトは可能な限り、いろんな考えを説明する方針であるため）。
　先ほどと同じようにコインAとコインBというようにコインに名前をつけます。そして、どのようなパターンがあるかを表にします。
表１　2枚のコインを投げたときのコインの状態

		コインA
		表	裏
コインB	表	表表	裏表
コインB	裏	表裏	裏裏

　この表から、最低でも片方のコインが裏である無い確率は3/4であることがわかります。この方法は分かりやすくて良いですね。しかし、やっていることは、「余事象を使わない方法」と全く同じです（表を描いて、全ての確率を出しています）。

このページのトップへ

3.実際に数値を入れて確認する

　情報処理技術者試験は、実際に数値を入れて１つ１つ確認する（机上でプログラムを走らせる感じ）ということをしないと解けない問題は結構あります。
　なので、分からなかったら、数値計算するのはありでしょう。
　まずは、例を示します。

■問題：アプリケーションサーバとDBサーバが直列でつながれているシステムがある。2つのサーバの稼働率が同じである場合、サーバの稼働率とシステム全体での稼働率の関係を表したグラフは以下のア～エのうちのどれになるか？

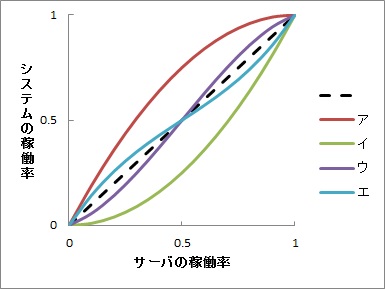
図１　サーバの稼働率とシステム全体での稼働率の関係
■正答：イ
■解説：
　まず、サーバの稼働率をx（0<x<1）とします。システム全体が稼働するためには、2つのサーバが稼動している必要がありますから、システム全体の稼働率をyとすると、
　　y = x * x
　　　= x ^ 2
　となります。
　
　問題はここからです。では、そのグラフはア～エのどれなのか？

◆まず、最も効率的で時間がかからない方法で解いています。
　y = x ^ 2です。二次関数ですね。なので、下に凸のグラフのグラフとなります。
　アは明らかに上に凸です。ウとエは下に凸と上に凸の両方がくっついていますから、違います。
　すると、残ったグラフであるイ（下に凸である）が答えとなります。
　しかし、この解答方法は、高校で数学IIICまでやっていないと難しいですね。それに、今回はこれで正解を得られましたが、常にこれだけで正解を得られる保障はありません。

◆次に、y = x ^ 2をxで微分、及び2回微分し、増減表を書き、どのグラフなのかを考えるやり方で解いてみます。
　まず、xで微分します。
　　y' = 2x
　y'が0となるときのxの値を求めるとx=0となります。
　さらに微分します。
　　y'' = 2
　y''が0となることはないことがわかります。そしてy''が常に正（どのxでも正）ですから、下に凸のグラフ（途中で上に凸になることがない）ということが分かります。
　ここから、増減表を作成します。
表２　増減表

	xの値
	-	0	+
yの値	＼	0	／
y'の値	-	0	+
y''の値	+	+	+

　ここから、アは上に凸なので違います（さらに付け加えると、x=0のときにy'=0となっていない）。ウとエはx=0.5の部分で上に凸と下に凸のグラフがつながっています。このような点を変曲点と言い、この場合、x=0.5においてy''=0となるハズですが、今回はそうではありません。なので、答えではありません。
　結局、残った、イが正解となります。
　しかし、この解答方法も、高校で数学IIICまでやっていないと難しいですね。ただし、この方法はこの手の問題ならどんなに複雑なグラフであっても対応できます。

◆最後に、実際に数値を入れて確認する方法で解いてみます。
　x = 0.5のとき（ただし、x = 1/2 のときとした方が計算が楽だろう）のyの値を求めます。
　もし、そのときのyの値が0.5より大きければ、アであり、小さければイ、0.5であればウかエです。
　もし、y = 0.5であった場合には、 x = 0.25のときのyの値を計算すれば良いでしょう。
　x = 0.5のとき、y = 0.25であるため、0.5より小さいですね。なので答えはイです。
　今回はxとyの関係が簡単なので、値の計算も簡単でしたが、常にそうだという保障はありません。

このページのトップへ

4.2進数の計算をそのまま行わない

　情報処理技術者試験では2進数の計算が出題されます。割り算の出題は無いと思いますが、足し算、引き算、掛け算は出題されます。
　基本的には2進数のまま計算するのですが、他の方法ですることができないか考えました。他の方法と言っても、たいした方法ではありませんが。
■問題：(1.11)₂ + (11.1)₂を計算せよ。
■正答：(101.01)₂
■解説：
◆まずは、2進数のまま計算する方法で解いてみます。
　では、筆算で。

			1	.	1	1
+		1	1	.	1

	1¹	0¹	1¹	.	0	1

　※注：繰り上がりは、上付き文字で表しています。

　よって答えは、(101.01)₂

◆次に、10進数に変換してから、足し算し、その後、2進数に直すという方法で解いてみます。
　(1.11)₂ = 1.75
　(11.1)₂ = 3.5
　よって、1.75 + 3.5 = 5.25
　これを、2進数に変換する。
　5.25 = (101.01)₂

　今回は、この方法でも時間がかかるということは無いですね。というか、2進数のまま行う方が、繰り上りが多く、大変でした。
　しかし、今回は、足し算だから、うまくいったと考えた方が良いです。引き算も大丈夫でしょうが、掛け算を10進数に変換してから行うのは、さすがにお勧めできません。

◆最後に、10進数表記の分数に直してから、足し算し、その後、2進数に直すという方法で解いてみます。
　

(1.11)₂ = 1 +

(11.1)₂ = 2 + 1 +

　2つを足すと、

となります。

　これを、10進数に直すと、(101.01)₂となります。
　今回は、3つの方法の中で最も効率が悪いですね。
　仮分数に直すのではなく、そのままの形（1 + 1/2 + 1/4とか）で計算という方法も考えられますが、2進数のままで計算するのと変わらなくなります。しかし、2進数のままで計算するのは理解できん、と言う方には、良いと思います。
　それから、掛け算の場合は、10進数表記の小数値で行うよりかは、この方法の方が楽に計算できると思います。

このページのトップへ

このページの利用によって発生した、いかなる損害について、このホームページの作成者は責任を負いません。
このページの間違いや嘘を見つけた方、このページに書いて欲しい情報がある方はメールをお願いします。

Microsoft 、Windows 、Visual Basic および Excel は米国Microsoft Corporationの米国およびその他の国における登録商標または商標です。
ここではExcel® をエクセル、Visual Basic® for Applications をVBAと表記する場合があります。
Mac 、Mac OS 、Mac OS X は米国Apple Computer,Inc.の登録商標または商標です。
その他、社名および商品名、システム名称などは、一般に各社の商標または登録商標です。

このホームページの作成者はこれらの会社とはいっさい関係がありません。