応用情報H24秋　問2の解説

作成日　2013/11/10
最終更新日　2013/11/16

　応用情報H24秋　問2の解説をします。

分野：テクノロジ系
大分類：基礎理論
中分類：基礎理論
小分類：応用数学

　まずは、与えられた条件から、式を立てます。

　食品Aの量をa[g]、食品Bの量をb[g]とします。
　すると、「成分1を70mg以上」という条件から、
　　　1 * a + 4 * b ≧ 70　・・・(1)
　という式が導出できます。
　次に、「成分2を80mg以上」という条件から、
　　　3 * a + 2 * b ≧ 80　・・・(2)
　という式が導出できます。

　次に、最終的に求める値を確認します。「成分3の最小摂取量」ですから、
　　　1 * a + 1 * b ≧ ?　・・・(3)
　の「?」の部分を、(1)と(2)の式から求めれば良いことになります。

　いくつかの方法を示します。自分にあった方法で解くのが良いでしょう。

◆数式から直接求める
　多分、最も時間がかからない方法です。その代わり、少し難しいかもしれませんが。

　方針としては、(1)と(2)の式から、
　　　X * a + X * b ≧ X * ?
　という式を作り、全体をXで割る（Xは正の数値とする）ことで、(3)の式を出すやり方です。

　(1)の式のaの項の係数は1、bの項の係数は4であり、差が3あります。
　(2)の式のaの項の係数は3、bの項の係数は2であり、差が1あります。

　ということで、(2)の式を3倍したものを、(1)の式に足し合わせます。すなわち、
　　　　1 * a + 4 * b ≧ 70
　　+)　9 * a + 6 * b ≧ 240
　　------------------------
　　　10 * a + 10 * b ≧ 310
　です。
　で、全体を10で割ると、
　　　a + b ≧ 31
　という式が出てきます。

　よって、答えはイです。

　不等式を式変形するときの注意
　不等式（>、<、≧、≦で結ばれた式）の式変形は等式（=で結ばれた式）の式変形よりも注意しなければならないことが多いです。
　以下に示します。まあ、間違えても、情報処理技術者試験程度では、問題は起きない（正解にたどり着ける）かもしれませんが。

全体に負の数値をかけた場合、あるいは、全体を負の数値で割ると、不等式（<、>、≧、≦）の向きが逆になります。
今回、2つの式を足し合わせましたが、同じようにして2つの式を引き算することは出来ません。
例えば、
　　　　1 * a + 4 * b ≧ 70
　　-)　3 * a + 2 * b ≧ 80
　　-----------------------
　　　-2 * a + 2 * b ≧ -10
の様は演算は、数学的に間違いです。
これが間違いであることは、具体的な数値を当てはめてみると良く分かります。
　　　　100 ≧ 70
　　-)　200 ≧ 80
　　-------------
　　　　-100≧-10
…。おかしいだろう。
引き算をしたら、不等号の向きを入れ替えればOKという考えもダメですよ。以下のケースも考えられるためです。
　　　　100 ≧ 70
　　-)　90 ≧ 80
　　-------------
　　　　10≧-10
とにかく、引き算は出来ないんです。

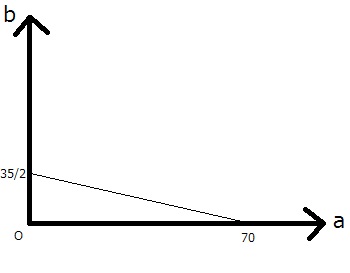
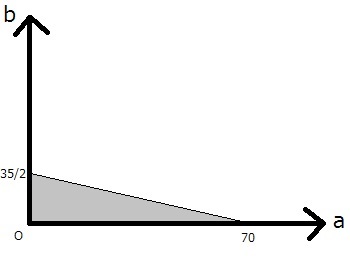
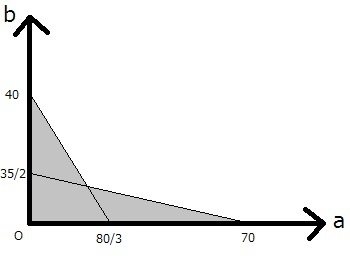
◆グラフを描いてみる
　面倒な方法ですが、直感的に解ける方法であり、恐らく、この方法が標準的な解き方だと思います。

　2つの不等式をグラフ化してみて考えてみよう（aが横軸、bを縦軸とします。逆でも良いのですが）。
　とりあえず、分からなかったら図を描いてみると良いでしょう。何かヒントが得られるかもしれません。

　早速、グラフを書くわけですが、書き方が分からない人がいるかもしれませんので、簡単にグラフの書き方を説明します。
　(1)の不等式で説明します。
　不等式のグラフを書くときは、まず、不等号の部分を等号に直します。すなわち、
　　　1 * a + 4 * b = 70
　です。
　次に、a = 0のときのbの値を求めます。同様に、b=0のときのaの値を求めます。
　　　a = 0のとき：　b = 35 / 2
　　　b = 0のとき：　a = 70
　そうしたら、上記2点を直線でつなげば良いわけです。
　グラフを描くと、次のようになります。

　注意：グラフはある程度正確に書きましょう。ある程度と言うのがあいまいですが、原点からa=70までの長さがb=35/2までのおおよそ4倍の長さになっていれば良いでしょう。
　実際には、(1)の式は等式ではなく不等式です。こういうときはaとbに適当な数字を入れて、成り立つかどうか調べます。
　とりあえず、a=0,b=0を代入すると
　　　1 * 0 + 4 * 0 ≧ 70
　で、式が成り立ちません。
　なので、「1 * a + 4 * b = 70」線で2つに切り分けられた範囲のうち、a=0,b=0が含まれない方の範囲が(1)のグラフになります。
　ここまでで、グラフは、

　となります。
　※灰色の部分は式が成り立たない範囲です。

　同様に、(2)の式もグラフに図示します。すると、

　となります。

　そうしたら、(3)のグラフを考えます。?の部分が分かりませんが、

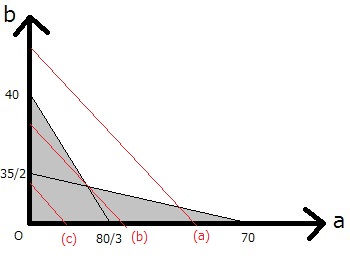
　の(a)、(b)、(c)のように、傾きが-1のグラフということだけは分かります。
　じゃあ、(a)、(b)、(c)のどれなのかですが、(1)、(2)のグラフの範囲（白い部分）が少しでもかぶる部分があるグラフの?を求めれば良いです。
　そうすると、(b)のグラフを求めれば良いです（が、そこまでしなくて良いです。(1)、(2)の線の交点を導出し、その値を(3)に代入すれば問題の答えが出ます）。
　※意味が分からなかったら、逆に考えましょう。(c)のグラフは(1)、(2)の不等式の範囲外ですから。ダメですね。(a)のグラフは範囲内ですが、ムダに大きいのです。

　ともかく、(1)と(2)の不等号を等号にした方定式（連立方程式）を解きましょう。すると、
　　　a = 18 , b = 13
　が出ます（連立方程式の解の導出の説明は省きます。中学レベルの数学だし。）。
　これを(3)の式(正確には不等号を等号にした式)に代入すると、
　　　a + b = 31
　が出ます。
　よって、答えはイです。

◆とにかく、連立方程式を解いてみる
　この方法は、（１）と（２）の式の不等号を等号にした式(連立方程式)、
　　　1 * a + 4 * b = 70
　　　3 * a + 2 * b = 80
　を解いて、得られた、aとbの値を 1 * a + 1 * b に代入して得られた値を答えにしてしまうという、少々乱暴な方法（数学的には良くない方法）です。

　少々、乱暴ですが、答えは得られます。
　実は、理由があるんです。

　数学、工学などにおいて、他と異なる部分と言うのは、問題の答えになっている場合が多いのです。
　今回は2つの方程式から引くことが出来る2つの線の交点の部分（それは連立方程式の解である）が答えになっています。
　午前試験は答えがあっていれば良いですから、分からなかったら、とりあえず、方程式を解いてみるのはありでしょう。

　もちろん、外す場合もありますが・・・。
　今回の問題だと、他と異なる部分というのは、a=0,b=40の点とa=70,b=0の点もそうなのです。

　そうそう、それから、「数学的には良くない方法」ということだけど、それは、まあ、分かって使う分には、気にしなくて良いでしょう。
　試験は時間との戦いというのもあるし。
　これを読んでいる人は文系大学出身の社会人が多いと考えています。そういう人は知らないと思うので説明すると、理系大学の受験でも数学的に良くない方法を使うとかあるから。
　ロピタルの定理は有名だよ（さすがに記述式の問題では使えないが、検算目的や答えだけ書く問題なら使える（使ったことがばれなければ使える））。
　ということで、理系大学の受験ですら、こうだから、たかが、情報処理技術者試験（しかも午前は選択問題だ）で気にする必要なしです。

このページのトップへ

このページの利用によって発生した、いかなる損害について、このホームページの作成者は責任を負いません。
このページの間違いや嘘を見つけた方、このページに書いて欲しい情報がある方はメールをお願いします。

Microsoft 、Windows 、Visual Basic および Excel は米国Microsoft Corporationの米国およびその他の国における登録商標または商標です。
ここではExcel® をエクセル、Visual Basic® for Applications をVBAと表記する場合があります。
Mac 、Mac OS 、Mac OS X は米国Apple Computer,Inc.の登録商標または商標です。
その他、社名および商品名、システム名称などは、一般に各社の商標または登録商標です。

このホームページの作成者はこれらの会社とはいっさい関係がありません。

応用情報H24秋　問2の解説

1.問題

2.解説

単位 mg
	成分1	成分2	成分3
食品A	1	3	1
食品B	4	2	1

応用情報H24秋 問2の解説

1.問題

2.解説

応用情報H24秋　問2の解説