作成日 2016/4/24
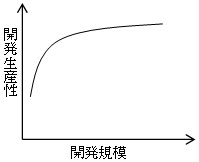
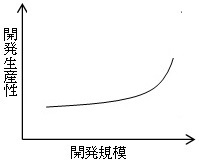
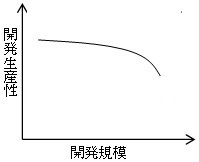
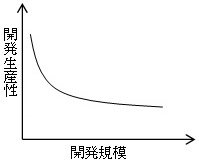
プロジェクトマネージャH28春 問11の解説
プロジェクトマネージャH28春 問11の解説をします。
1.12 1.12
このページの利用によって発生した、いかなる損害について、このホームページの作成者は責任を負いません。
このページの間違いや嘘を見つけた方、このページに書いて欲しい情報がある方は
メール をお願いします。
Microsoft 、Windows 、Visual Basic および Excel は米国Microsoft
Corporationの米国およびその他の国における登録商標または商標です。